在区块链领域,“ AMM”和“ Yield Farming”正火。如果你学得更深入,则会遇到另一个流行语-“无常损失(IL)”。考虑到它现在风靡一时,我认为了解其性质至关重要。你是否对以下问题有答案:
无常损失到底是什么?流动资金提供者如何遭受无常损失?影响流动性提供者可能遭受无常损失的主要因素有哪些?
在本文中,我将首先建立AMM无常损耗的数学模型。然后,在整个数学分析中,你将学习AMM收益农耕中的每个主要因素如何影响流动性提供者可能经历的IL规模。
什么是无常损失?
简而言之,无常损失是指将代币存储在AMM中与将代币存储在钱包中之间的区别。当AMM中的代币价格在任何方向上发生偏离时,就会发生这种情况。差异越大,无常损失越大。
为什么“无常”?
因为只要你进入AMM时AMM中代币的相对价格恢复到其原始状态,损失就消失了,你可以获得100%的交易费用。但是,这种情况很少发生。通常,无常损失会变成永久性损失,吞噬你的交易收入或使你获得负收益。

尽管去年LINK上涨了700%以上(以美元计),但在Uniswap上为LINK / ETH提供流动性的回报却下降了-52.67%。
它如何发生?
要了解无常损失的发生方式,我们首先需要了解AMM定价的工作方式以及套利者的作用。原始形式的AMM与外部市场脱节。如果外部市场上的代币价格发生变化,则AMM不会自动调整其价格。它需要套利者来购买低价资产或出售高价资产,直到AMM提供的价格与外部市场匹配。
在此过程中,套利者提取的利润从流动性提供者的口袋中有效地去除了,导致了无常损失。例如,假设一个AMM具有两个资产,ETH和DAI设置为50/50的比率。如下所示,以太坊价格的变化为套利者提供了以牺牲流动性提供商为代价获利的机会。

如果查看不同的价格变动,你会发现,即使ETH价格发生微小变化,也会导致流动性提供者遭受无常损失:
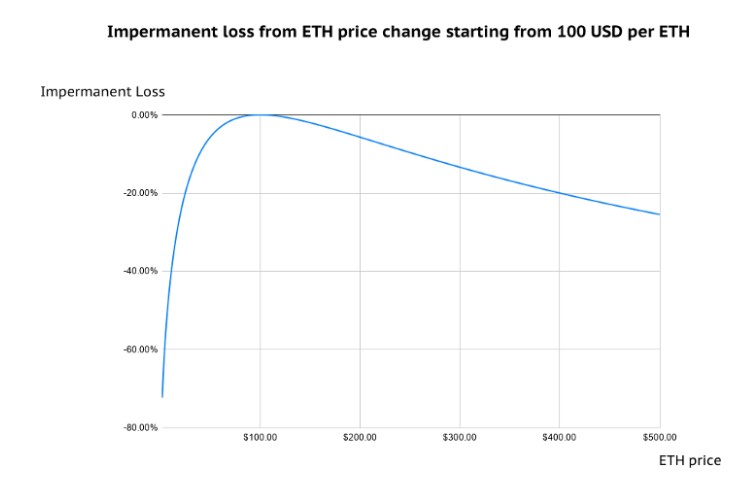
显然,如果AMM要在日常用户和机构中广泛采用,则需要解决此问题。如果希望用户不断监控AMM的变化并采取行动以免造成重大损失,则流动性准备金将成为仅适用于最高级交易者的游戏。与其设计第二层工具来监视和管理AMM风险,不如尝试在协议级别上减轻无常的损失?
我们如何减轻无常损失?
幸运的是,该行业正在与无常损失作斗争。这一进步始于认识到,如果我们可以最大程度地降低AMM中代币价格之间的差异,就可以降低无常损失的风险。如果AMM中的代币之间的相对价格保持不变(假设它们中没有一个失败),那么流动性提供者承担的风险就较小,并且可以对交易费用实际上使他们获利更有信心。因此,事实证明,具有“镜像资产”(或保持恒定价格比的代币)的AMM对无常性损失具有特别的弹性,由于其利润优化的结构而吸引了大量的流动性。
其中包括Uniswap上的sETH / ETH之类的AMM,以及Curve上的DAI / USDC / USDT / sUSD等基于稳定币的AMM。

由于ETH和ETH价格之间几乎没有差异,因此ETH / ETH AMM的无常损失微不足道。资料来源:ZumZoom
但是,具有镜像资产的AMM固有地仅限于稳定币或包装和合成代币。此外,用户无法维持其多头头寸,而是在提供流动性时必须持有额外的“储备”资产。
Bancor V2于2020年7月推出,旨在通过将镜像资产AMM的概念扩展到易失性代币来解决这些问题。通过与Chainlink价格预言机集成,Bancor V2可以创建具有固定流动性储备的AMM,以期使代币的相对价值保持恒定。预言机被用来调整资金池的权重和费用,以激励套利者在出现赤字时将价值带回资金池,从而减轻稳定代币和易失性代币的无常损失。至关重要的是,这种设计还允许用户提供流动性,而无需持有额外的包装资产或合成资产。取而代之的是,你可以通过AMM中的单个代币提供100%的敞口流动性。

Bancor V2可以创建具有固定流动性储备的AMM。这种类型的AMM保持其储备金的相对价值不变,从而降低了无常损失的风险。
让我们建立一个数学模型
考虑一个简单的AMM流动资金池中最一般的情况,其中:I.总共有两种类型的代币-代币A和代币B;二。这两个代币之间的汇率或价格由不变产品模型确定;三,流动性提供者可以获得的唯一奖励是池的交易费。粗略地说,在分配UNI代币之前,只需将我们的AMM视为Uniswap。

一个简单的AMM流动资金池
最一般的情况如下:该池当前具有x个A代币和y个B代币。它们之间的价格为α。换句话说,1 A代币=αB代币。
作为此池的新流动性提供者,你拥有p个A代币和q个B代币。如果价格为α,则p A代币的总价值和q B代币的总价值相同。然后,你将流动性对放入该池中。结果,该池现在具有(x + p)个A代币和(y + q)B个代币,汇率保持为α。

最一般的情况
由于价格在整个过程中保持为α,因此上述情况可以转换为一种更简单但等效的情况:(i)该池当前具有(x + p)个A代币和(y + q)B个代币,价格为α(ii)你为此池贡献的流动性,为p A代币和q B代币;换句话说,你的贡献等于整个池的p /(x + p)或等效地q /(y + q)。

比较简单但等效的一个
由于交易费用是根据其对资金池的贡献按比例分配给流动性提供者(LP),因此该模型可以从多个LP简化为一个LP。此后,我们的模型变为:你提供一个x A代币和y B代币的流动性对,以创建一个新的流动性池。根据固定产品价格机制,A代币的价格相对于B代币的价格为α。

模型简化为一个单一的流动性提供者
为了使其在数学上更易于管理,我们将“价格为α的x A个代币和y B代币”视为“ c个单位代币对”,其中一个单位代币对由一个A代币和αB代币组成。因此,我们用矢量1 A,αB表示一个单位代币对,并且该池当前具有c 1 A,αB或c A,cαB。

向量化后的模型
这是我们池的初始状态。如果发现符号令人困惑,则将A代币视为ETH,将B代币视为DAI,并将α的价格视为DAI。那么,c A,cαB的简单含义是:池中有c A个代币和cαB个代币,其中α是价格。
模型完成,现在让我们交换!
现在,考虑与B代币有关的A代币的市场价格已从α变为α+δ,其中δ可以为正也可以为负。感知潜在利润的套利者Alice将一些A代币交换为B代币(反之亦然,取决于δ是正还是负),并将我们池中的价格从α变为α+δ。换句话说,在Alice掉期之后,该池中的价格现在变为:1 A =α+δB。
假设你作为储备库的唯一流动性提供者,从Alice的掉期交易中获得了t美元兑换美元的交易费:你在我们的小型储备库中通过收益农业获得了t美元。这是赚钱的一面。
现在,让我们考虑失败的一面。你无需保留A代币和B代币到小池中,而只需持有代币,价格变动后A代币和B代币的总价值为(c *(α+δ)+cα)B代币,因为现在1 A =α+δB。如果1 B =ξ美元,则你将有((α+δ)+α)* c *ξUSD。
但是,在这种情况下,你没有持有代币,而是将其作为流动性提供给我们的资金池。因此,在价格变动和Alice掉期之后,你不再拥有c A代币或cαB代币。例如,如果δ为正,你将拥有更多的B代币和更少的A代币,因为Alice已经用B代币交换了一些A代币。
然后,通过求解涉及x,y,A,B,α,δ,c的三个简单数学方程式,可以计算出A代币和B代币的确切数量。这样做,你将获得c * sqrt(α/α+δ)A标记和c * sqrt(α*α*(δ))B标记(强烈建议你直接解决它们,因为等式非常简单) 。如果像以前一样1 B =ξ美元,现在你有2 * sqrt(α*(α+δ))* c *ξUSD。将其与持有代币所获得的金额进行比较,净差为2 * sqrt(α*(α+δ))* c *ξ—((α+δ)+α)* c *ξ =-(sqrt(α)-sqrt(α+δ))?* c *ξ。由于c和ξ均为正,因此净差始终为正。换句话说,只要δ不为零,即价格有变化,你就有亏损的一面。
至此,我们已经完成了你失败的一面。现在让我们一起考虑双方:你的最终IL =价格变动损失-交易费收入。因此,IL =(sqrt(α)-sqrt(α+δ))2 * c *ξ-t。
仔细研究IL公式
现在,我们已经从宏级别计算了IL公式。但是由于我的模型基于简单的AMM流动性池中的简单案例,该公式仍然非常通用。因此,要真正理解该公式的含义,我们需要仔细研究并分析哪些因素会影响我们的IL,以及它们如何影响。
让我们再次写出公式:IL =(sqrt(α)-sqrt(α+δ))?* c *ξ— t
由此,我们可以得出以下结论:如果你赚取更多的交易费t,你的IL将会减少。如果你增加流动性准备金,那么你还将线性增加IL(在公式中的参数c中显而易见)。
一个B代币的价值越高,你将遇到的IL就越多(如公式中的参数ξ所示)。因此,例如,一个wBTC-ETH池比一个wBTC-DAI池可能具有更密集的IL,因为一个ETH比一个DAI更有价值。
如果相对于B代币而言,相对于B代币而言,A代币的初始价格α高,则你将体验到更少的IL(在“ sqrt(α)-sqrt(α+δ)”中显示)。这是因为,如果α与δ相比非常大,则总计(sqrt(α)-sqrt(α+δ))?,而产生的IL将非常小。
那么,作为流动性提供者,如何减少潜在的无常损失?
首先,找到交易费用最高的池,或者找到其他奖励的池。这将使你扩展收入方面。其次,当你增加流动性准备金时,请记住潜在的无常损失也呈线性增长。第三,选择代币价值低于美元的池。最后也是最重要的是,选择价格波动尽可能小的池。
原文作者:Zhou(Joe) Yu, Sperax.io加州大学洛杉矶分校计算与哲学数学的顶级研究员
原文链接:Defi Series: Impermanent Loss — How AMMs Mathematically Determine it?